Fejér Lipót kézzel írott válaszlevele Goldberger Leónak

Budapest, 1943. január 22.

Mélyen Tisztelt Kedves Barátom!

Köszönöm szíves soraidat és az érdekes tétel közlését. Én nem is hallottam ezt soha. Meggyőződtem róla, hogy 142857 valóban az egyetlen hatjegyű szám, amely a szóban forgó tulajdonsággal bír.

Feladat. Keressünk egy tízes-rendszerbeli hatjegyű egész számot x = abcdef, amely a következő három tulajdonsággal bír:
1.) az a, b, c, d, e, f jegyek egyike sem egyenlő zérussal,
2.) az a, b, c, d, e, f jegyek egymástól különbözők
3.) az x, 2x, 3x, 4x, 5x, 6x mind hatjegyű számok, amelyek mind ugyanazon a, b, c, d, e, f jegyekkel írhatók fel, és pedig így:
                           x = a b c d e f                                     I.
                                 b c d e f a                                     II.
                                 c d e f a b                                     III.
                                 d e f a b c                                     IV.
                                 e f a b c d                                     V.
                                 f a b c d e                                     VI.
(A kívánalom [követelés] nem úgy értendő, hogy itt a második sor adja a 2x-et, a harmadik a 3x-et stb., hanem csak úgy, hogy a fenti hat szám az x, 2x, 3x, 4x, 5x, 6x-et adja valamely egymásutánban.)

Megjegyzés (pusztán egy matematikai műszó felemlítése). A második, harmadik, ..., hatodik sorban fölírt betűk az első sorban lévő a, b, c, d, e, f hat betű ú. n.

adják, és pedig mely permutációit? - az ú. n.

cyclikus permutációit.

	[X] Hat elemnek összesen csak 6 cyclikus permutációja van; az összes permutációk száma 1*2*3*4*5*6

(Honnan ez az elnevezés: cyclikus? Ha egy kört rajzolsz, és megjelölsz ezen, a nyíl által jellemzett természetes sorrendben hat pontot, a, b, c, d, e, f-et

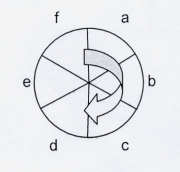
akkor : ha a-nál kezded és körüljárod a kört, kapod: a b c d e f, ha b-nél kezded és körüljárod a kört, kapod: b c d e f a stb. - rendre a fenti hat „cyclikus permutációt".)

Már most kérdésünk legpregnánsabban úgy fogalmazhatjuk meg, hogy keresendő egy, az 1.), 2.) föltételeknek megfelelő x = a b c d e f hatjegyű szám úgy, hogy 3.) az x, 2x, 3x, 4x, 5x, 6x számok számjegyei megadják az a b c d e f cyclikus permutációinak teljes 6-tagú rendszerét (valamely sorrendben). (A 7-tel való szorzásról egyelőre hallgatunk.)

Azt állítottam, csak ismétlem, hogy x = 142 857 az egyetlen hatjegyű szám, amely az 1.), 2.), 3.) föltételeknek megfelel.

Bizonyítás. Világos, hogy az a = 1. Ha ugyanis a = 2, 3, ..., 9 volna, akkor 6x egymilliónál nagyobb volna, tehát nem volna hatjegyű szám.

Tehát
x = 1 b c d e f.
Az első jegy tehát meg van határozva.

Most a hatodik jegyet, az f-et fogom meghatározni. Azt állítom, hogy f nem lehet páros jegy (vagyis 2 vagy 4 vagy 6 vagy 8). Mert akkor 2x, 3x, 4x, 5x, 6x is vagy 0-sal vagy 2-vel vagy 4-gyel vagy 6-tal vagy 8-cal végződnék, tehát egyszer sem 1-gyel. Mivel pedig 1, mint láttuk, az x egyik jegye (az első), kell, hogy (a cyclikusság folytán) a többszörösök egyike az 1 jeggyel végződjék. Eszerint csak
f = 1 vagy 3 vagy 5 vagy 7 vagy 9
lehetséges.

Ámde f = 1 nem lehet, mert akkor az 1 jegy kétszer fordulna elő a keresett x-ben, amit kizártunk. Maradnak az
f = 3, 5, 7, 9
lehetőségek.

Most képezzük a 2x, 3x, 4x, 5x, 6x-et. Elhagyhatjuk a 2x, 4x, 6x páros többszörösöket, mert azok csak páros jeggyel, tehát 1-gyel nem végződhetnek. Marad a két többszörös:
3x, 5x

Minthogy
x = · · · · · f,
(ahol, mint mondottuk, f = 3 vagy 5 vagy 7 vagy 9), tehát 3x vagy 9-cel vagy 5-tel vagy 1-gyel vagy 7-tel végződik (tehát csak az f = 7 esetben 1-gyel). Viszont 5x mind a négy esetben 5-tel végződik.
Látjuk tehát, hogy az x = 1 b c d e f számra nézve a 2x, 3x 4x, 5x, 6x számok valamelyike akkor és csak akkor végződhetik 1-gyel, ha f = 7 (Ekkor 3x = · · · · · 1).

Tehát most már mondhatjuk, hogy szükségképpen
x = 1 b c d e 7,
vagyis a keresett szám első és hatodik jegyét meghatároztuk.

Most, drámai gyorsasággal, meg tudom határozni a még ismeretlen négy jegy lehetséges értékét (ha nem is mindjárt a helyöket is). Ugyanis az x imént nyert alakjából nyilván következik:
  x = · · · · · 7
2x = · · · · · 4
3x = · · · · · 1
4x = · · · · · 8
5x = · · · · · 5
6x = · · · · · 2
Minthogy követeljük, hogy mind a hat jegy egyszer és csak egyszer utolsó jegye legyen a hat darab hatjegyű x, 2x, 3x, 4x, 5x, 6x számok valamelyikének, tehát a mi keresett számunk szükségképpen az imént talált
1, 2, 4, 5, 7, 8
jegyekből áll. Csak az a kérdés, hogy melyik helyen áll ez a talált hat jegy? Az 1-ről már tudjuk, hogy (balról) az első helyen áll, és a 7-ről már tudjuk, hogy (balról) a hatodik helyen áll. De mi van a 2, 4, 5, 8 jegyek helyével?

Azt állítom először is, hogy az 5 jegy az ötödik helyen áll. Vagyis, hogy
x = 1 · · · 57
Ha ugyanis nem az 5 állna az ötödik helyen, akkor a három most posszibilis jegy közül a 2 vagy a 4 vagy a 8 állana ezen az ötödik helyen.

Ez azonban nem felel meg, amit a következőképpen bizonyítok be.

α) Ha ugyanis
  x = · · · · 27
volna, akkor
2x = · · · · 54
3x = · · · · 87
4x = · · · · 08
Íme 4x-ben föllépett a szerepléstől eltiltott 0 jegy. Tehát x = · · · · 27 nem felel meg.
Ha meg x = · · · · 47
volna, akkor

β)
2x = · · · · 94

Minthogy a 9 jegy szintén nem szerepelhet egyik többszörösben sem, tehát x = · · · · 47 sem válik be.
Végre, ha
γ)
x = · · · · 87
volna, akkor
2x = · · · · 74
3x = · · · · 67
Minthogy a 6 jegy szintén nem szerepelhet, tehát az x = · · · · 87 sem válik be.

Tehát tényleg az 5-ik helyen csak az 5 jegy állhat, vagyis addig jutottunk el, hogy
x = 1 b c d 5 7

Most egy pár sor, és a végén vagyunk.
Ezután a 8 jegy helyét keresem a még rendelkezésre álló három hely közül.
x = 18 · · 57
nem válik be, mert most 6x több, mint egymillió, és így több, mint 6 jegyből állana.

Megpróbáljuk tehát, hogy
x = 1 · 8 · 57
megfelel-e? csak két lehetőség van:
vagy:                              x = 1 2 8 4 5 7
vagy:                              x = 1 4 8 2 5 7

Egyik sem válik be. Ugyanis az első esetben
2x = · · · 914
a második esetben pedig
2x = · · 6514.
De 9, illetőleg 6 nem szerepelhet mint jegy. Tehát 8 nem lehet a harmadik helyen sem.

Marad, mint utolsó lehetőség:
x = 1 · · 857.
Ezután már csak két szám közül kell választanunk; az egyik
x = 1 2 4 8 5 7,
a másik
x = 1 4 2 8 5 7.
Az első nem válik be; ugyanis
2x = · · 9714
-ben a meg nem engedett 9-es jegy lép föl.
Végre marad
x = 1 4 2 8 5 7
mint egyetlen hatjegyű szám, amely a mi 1), 2), 3) követelésünknek eleget tehet.

Mondom, ezzel az van bebizonyítva, hogy az összes 6-jegyű, egymástól különböző jegyű, zérus jeggyel nem bíró számok között az x = 1 4 2 8 5 7 az egyetlen, amelyre nézve a 2x, 3x, 4x, 5x, 6x többszörösök jegyhatosai az eredeti 1, 4, 2, 8, 5, 7 számhatos többi 5 cyclikus permutációját adhatják. Hogy tényleg szolgáltatják, azt a szorzás mutatja:
x = 1 4 2 8 5 7                                                              I.
2x = 2 8 5 7 1 4                                                            III.
3x = 4 2 8 5 7 1                                                            II.
4x = 5 7 1 4 2 8                                                            V.
5x = 7 1 4 2 8 5                                                            VI.
6x = 8 5 7 1 4 2                                                            IV.
(A jobb oldalon álló római számok jelzik, hogy az 1. oldal értelmében hányadik cyclikus permutáció áll elő, ha x-et rendre 1, 2, 3, 4, 5, 6-tal megszorozzuk.)

Ezzel a feladatot megoldottuk.
Megjegyzem, próbáltam 3-jegyű számot találni, amely a mi x számunkkal analóg tulajdonságot mutat. hamarosan kiderült, hogy ilyen 3-jegyű szám nincs.

Adjuk össze a fenti hat számot; kapjuk, minthogy minden oszlop is az 1 4 2 8 5 7 jegyekből áll,
21x = (1+4+2+8+5+7) * (10⁵+10⁴+10³+10²+10+1) = 27*111 111,
vagyis, osztva mindkét oldalt 3-mal
7x = 9*111 111 = 999 999.

Látható ebből, hogy a 7-tel való szorzásra vonatkozó állítás már csak következménye az x, 2x, 3x, 4x, 5x, 6x-re vonatkozólag követelt „cyclikus" tulajdonságnak.

Én remélem, hogy amit írtam, meg lehet érteni. Ha valamely pont nehézséget okoz, akkor fordulj kedves tanítványomhoz, Popper Edit kisasszonyhoz, akit egy kis, esetleg szükséges magyarázat adására ezennel ünnepélyesen megkérek. A Méltóságos asszonynak tisztelettel kézcsókomat küldöm, Téged pedig, mint egyéniséged és nagy műved - annyi sok között - egyik igaz tisztelője, a semmeringi együttlétre is gondolva, szeretettel köszönt
Fejér Lipót